Kyle Corry

Projects Research Recipes

Offline Global Tide Predictions

2024-11-29

In this article, I’ll cover the system used in Trail Sense that enables offline tide prediction at any coastal location.

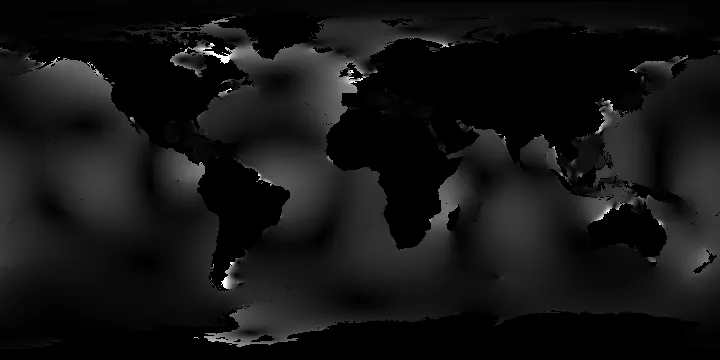M2 harmonic amplitude The M2 harmonic constituent amplitude from EOT20

Background

Tidal harmonics

Tides can be represented by "harmonic constituents," which are a series of waves defined by their amplitudes, phases, and speeds. By combining these waves, we can generate a final waveform that represents the water level. The times of high and low tide can be determined as the local extrema of this waveform.

Harmonic constituents correspond to real-world factors such as the position of the Earth relative to the Sun and Moon, as well as shallow-water interactions. Constituents are defined by a constant speed, which represents the frequency of the associated wave. For example, the S2 (solar semidiurnal) speed is 30 degrees / hour, which corresponds to a 12 hour period (half a day). The phase and amplitude of each of these constituents varies by location and are calculated through frequency analysis of water level.

Before the tidal harmonics can be transformed into water levels, a correction/reference for each constituent wave needs to be calculated. These factors let us choose a reference start date (say January 1, 2025 0h UTC) and they account for changes to the Sun-Earth-Moon system over time. Once we choose a start date, we can precompute and embed these as constants.

For each constituent, the following information is required:

Finally, the water level can be calculated as follows:

t = (currentTime - jan_1_2025_0utc).seconds level = 0 for c in constituents level += c.f * c.amplitude * cos(c.speed * t + c.V + c.u - c.phase)

Solution

Image generation

  1. Download the EOT20 tide data. [1]
  2. Download a land mask from Natural Earth. [2]
  3. Dilate the land mask to include ocean regions near the coastlines.
  4. Use the land mask to remove excess ocean tide data from the EOT20 tide model.
  5. Resize the resulting image to 720x360 (2 pixels per degree of latitude/longitude).
  6. Remap the amplitudes and phases to values between 0 and 255, recording the maximum amplitude for each factor. Amplitudes over 500 cm are handled separately to retain sufficient resolution (these are rare).
  7. Remove all land and open ocean pixels (leaving just the coastline) and resize the resulting array to have a width of 250 pixels. This results in compressed images for both amplitude and phase, albeit with a loss of spatial information.
  8. To recover spatial information, replace each pixel in the 720x360 image with the X (red) and Y (green) coordinates of its position in the compressed image. Use a 1-based indexing system, where RGB = 0 indicates irrelevant pixels. Export this as a lossless WebP file.
  9. Store each compressed amplitude image in the red, green, and blue channels of a lossless WebP file. Repeat this for the compressed phase images.

The resulting images are under 300 KB in size.

Harmonic lookup

  1. Convert the latitude and longitude to a pixel location (2 pixels per degree).
  2. Load an 11x11 region of the indices image, centering the desired pixel. Handle wrapping on the X-axis. The size of this is adjustable depending on how far from the coast you want to display a tide.
  3. Find the nearest non-black pixel to the center of the region.

  4. Extract the X and Y coordinates of the compressed images: X = pixel.red - 1 Y = pixel.green - 1

  5. For each amplitude and phase file, load the X, Y pixel. Map it from [0, 255] to [0, max amplitude for constituent] and [-180, 180] respectively. You now have the harmonic constituents for the location, which can be plugged into the tidal harmonic formula to obtain the water level and extremas can be located to get the time of high/low tide.

Results

Using a test dataset of 27 locations (covering all 7 continents and 5 oceans) and 30 days (spanning all 4 main phases of the Moon), the following results were obtained:

This level of accuracy is sufficient for my use case. However, increasing the resolution of the tide images would reduce errors at the cost of a larger storage footprint.

Source code

References

  1. Hart-Davis Michael, Piccioni Gaia, Dettmering Denise, Schwatke Christian, Passaro Marcello, Seitz Florian (2021). EOT20 - A global Empirical Ocean Tide model from multi-mission satellite altimetry. SEANOE. https://doi.org/10.17882/79489

  2. Made with Natural Earth. Free vector and raster map data @ naturalearthdata.com.